planta: sistema a controlar
controlador: Provee la excitación de la planta; Se diseña para controlar el comportamiento de todo el sistema
La función de transferencia del controlador PID es:

Kp = Ganancia Proporcional
KI = Ganancia Integral
Kd = Ganancia Derivativa
Primero, hecharemos un vistazo a cómo trabaja el controlador PID en un sistema a lazo cerrado usando el esquema de abajo. La variable (e) representa el error de seguimiento, que es la diferencia entre el valor deseado de entrada (R) y la salida real (Y). Esta señal de error (e) será enviada al controlador PID , y éste calculará tanto la derivada cuanto la integral de esta señal de error. La señal (u) recién salida del controlador es ahora igual a la ganancia proporcional (Kp) veces la magnitud del error más la ganancia integral (Ki) veces la integral del error, más la ganancia derivativa (Kd) veces la derivada del error.

La señal (u) se enviará a la planta, y se obtendrá la nueva salida (Y). Esta nueva salida (Y) se re-enviará al sensor para hallar la nueva señal de error (e). El controlador toma esta nueva señal de error y computará su derivada y su integral otra vez. Este proceso sigue sin parar.
Las caracteristicas de los controladores P, I, y D
Un controlador proporcional (Kp) tendrá el efecto de reducir el tiempo de elevación y reducirá ,sin jamás eliminar, el
error de estado estacionario . Un control integral (Ki) tendrá el efecto de eliminar el error de estado estacionario, pero puede empeorar la respuesta transitoria. Un control derivativo (Kd) tendrá el efecto de incrementar la estabilidad del sistema, reduciendo el sobrepico, y mejorando la respuesta transitoria. Los efectos de cada uno de los controladores Kp, Kd, y Ki en un sistema a lazo cerrado se resumen en la tabla de abajo.
la L Cerrado T.TREPADA SOBREPICO T Establecim. ERROR (SS)
Kp Baja Sube poco Cambio Baja
Ki Baja Sube Sube Elimina
Kd Poco Cambio Baja Baja Poco Cambio
que estas correlaciones podrían no ser exactamente seguras, porque Kp, Ki, y Kd son dependientes entre sí. De hecho, cambiando una de estas variables se puede variar el efecto de las otras dos. Por esta razón, la tabla deberá usarse únicamente como referencia cuando se determina los valores de Ki, Kp y Kd.
Problema Ejemplo
suponga que tenemos un problema de masa simple, resorte,y amortiguador

La ecuación de modelo de este sistema es :

Tomando transformada de Laplace de la ecuación del modelo (1) :

La función de transferencia entre el despalzamiento X(s) y la entrada F(s) es entonces :

Sea :
M = 1kg
b = 10 N.s/m
k = 20 N/m
F(s) = 1
Introduzca estos valores en la función de transferencia anterior

El objetivo de este problema es mostrarle cómo contribuyen Kp, Ki y Kd para
Menor tiempo de subida
Mínimo sobrepico
Error de estado estacionario nulo
Respuesta a lazo abierto al escalón
Veamos primero la respuesta a lazo abierto al escalón. Cree un nuevo archivo-m y agregue el siguiente código:
num=1;
den=[1 10 20];
step(num,den)
Corriendo este archivo-m, la ventana de comandos del Matlab le debería dar la figura de abajo
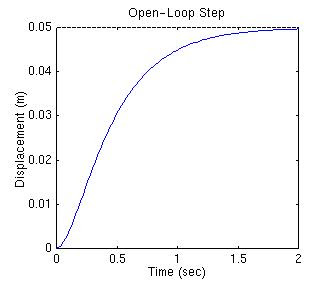
La ganancia de continua de la función de transferencia de la planta es 1/20, así que 0.05 es el valor final de la salida a una entrada escalón unitario. Esto se corresponde al error de estado estacionario de 0.95, bastante grande de hecho. Además, el tiempo de elevación es alrededor de un segundo, y el tiempo de establecimiento es alrededor de 1.5 segundos. Diseñemos un controlador que reducirá el tiempo de elevación y el tiempo de establecimiento, y eliminará el error de estado estacionario.
Control proporcional
De la tabla de arriba, vemos que el controlador proporcional (Kp) reduce el tiempo de trepada, incrementa el sobrepico, y reduce el error de estado estacionario. La función de transferencia a lazo cerrado del sistema de arriba con un controlador proporcional es:

Iguale la ganancia proporcional (Kp) a 300 y cambie el archivo-m con lo siguiente:
Kp=300;
num=[Kp];
den=[1 10 20+Kp];
t=0:0.01:2;
step(num,den,t)
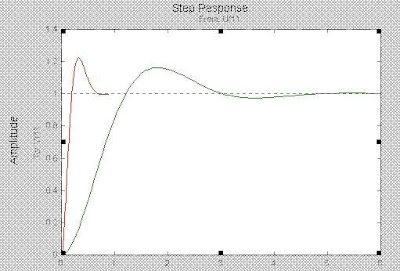
Corriendo este archivo-m, la ventana de comandos del Matlab le da la figura siguiente

Note: Puede usarse la función cloop para obtener la función de transferencia a lazo cerrado directamente de la función de transferencia a lazo abierto (en lugar de obtenerla a mano). El siguiente archivo-m usa el comando cloop que le debería dar un gráfico similar al de abajo.
num=1;
den=[1 10 20];
Kp=300;
[numCL,denCL]=cloop(Kp*num,den);
t=0:0.01:2;
step(numCL, denCL,t)
El gráfico de arriba muetra que el controlador proporcional redujo tanto el tiempo de elevación cuanto el error de estado estacionario, incrementando el sobrepico, y bajando el tiempo de establecimiento en pequeña medida.
Control Proporcional-Derivativo
Ahora, echemos un vistazo a un Control PD. De the table de arriba, vemos que el controlador derivativo (Kd) reduce tanto el sobrepico cuanto el tiempo de establecimiento. La función de transferencia a lazo cerrado del sistema dado con un Controlador PD es:

Haga Kp igual a 300 como antes e iguale Kd a 10. Ingrese los siguientes comandos en un archivo-m y ejecútelo en la ventana de comandos del Matlab.
00;
Kd=10;
num=[Kd Kp];
den=[1 10+Kd 20+Kp];
t=0:0.01:2;
step(num,den,t)
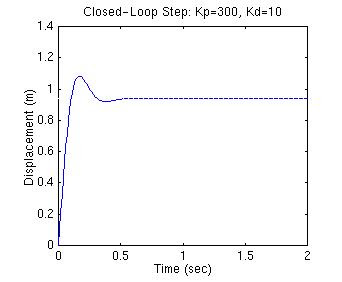
Esta figura muestra que el controlador derivativo redujo tanto el sobrepico cuanto el tiempo de establecimiento, y tuvo poco efecto en el tiempo de elevación y el error de estado estacionario.
Control Proporcional-Integral
Antes de avanzar a un control PID, echemos un vistazo al Control PI. De la tabla, vemos que un controlador integral (Ki) decrementa el tiempo de elevación, incrementa tanto el sobrepico cuanto el tiempo de establecimiento, y elimina el error de estado estacionario. Para el sistema dado, la función de transferencia a lazo cerrado con un Control PI es:

Reduzcamos Kp a 30, y hagamos Ki igual a 70. Cree un archivo-m nuevo e ingrese los siguientes comandos.
Kp=30;
Ki=70;
num=[Kp Ki];
den=[1 10 20+Kp Ki];
t=0:0.01:2;
step(num,den,t)
Corra este archivo-m en la ventana de comandos del Matlab, y obtenga la figura siguiente.

Control Proporcional-Integral-Derivativo
Ahora, echemos un vistazo a a controlador PID . La función de transferencia a lazo cerrado del sistema dado con un controlador PID es:

Luego de varias ejecuciones de prueba y error, las ganancias Kp=350, Ki=300, y Kd=50 proveerán la respuesta deseada. Para confirmarlo, ingrese los siguientes comandos en un archivo-m y ejecútelo en la ventana de comandos. Debería obtenerse la siguiente respuesta al escalón .
Kp=350;
Ki=300;
Kd=50;
num=[Kd Kp Ki];
den=[1 10+Kd 20+Kp Ki];
t=0:0.01:2;
step(num,den,t)

Ahora, obtuvimos el sistema sin sobrepico, rápido tiempo de subida, y error de estado estacionario cero.
Sugerencias generales para el diseño del controlador PID
Cuando está diseñando un controlador PID para un sistema dado, siga los pasos de abajo para obtener una respuesta deseada.
Obtenga una respuesta a lazo abierto y determine qué hay que mejorar
Agregue un control proporcional para mejorar el tiempo de elevación
Agregue un control derivativo para mejorar el sobrepico
Add an control integral para eliminar el error de estado estacionario
Ajuste cada coeficiente Kp, Ki, y Kd hasta que obtenga la respuesta general deseada. Puede mirar en la tabla de este "Tutorial PID" para averiguar cuál controlador controla cierta característica.
Finalmente, tenga en mente que no implementará los tres controladores (proporcional, derivativo, e integral) en un sistema, si no es necesario. Por ejemplo, si el controlador PI le proporciona una buena respuesta (como el ejemplo anterior), no necesitará implementar un controlador derivativo . Mantenga el controlador lo más simple que se pueda.