Un sistema de control se especifica en términos de dicha respuesta transitoria para una entrada escalón unitario, puesto que es fácil de generar, y si se conoce la respuesta al escalón, es matemáticamente posible calcular la respuesta para cualquier entrada. La respuesta transitoria de un sistema para una entrada escalón unitario depende de las condiciones iniciales, usando en muchas ocasiones la condición inicial nula, para lo cual la salida y todas las derivadas con respecto al tiempo son cero, y el sistema se analiza con mayor facilidad, aunque es importante conocer el efecto de las condiciones iniciales sobre la respuesta del sistema.
Esta respuesta de un sistema de control práctico muestra con frecuencia oscilaciones amortiguados antes de alcanzar el estado estacionario.
Para ello, presentamos a contincaracterísticos como son la frecuencia natural no amortiguada (wn ) y el coeficiente de amortiguamiento( x ).Un sistema de segundo orden tiene como función de transferencia a la siguiente ecuación:
uación los tipos de respuesta que puede presentar un sistema de segundo orden, a través del estudio de su función de transferencia, y de sus parámetros
donde: ωn: frecuencia natural no amortiguada y ξ: coeficiente de amortiguamiento.La respuesta del sistema depende de las raíces del denominador (polos del sistema). Para un sistema de segundo orden los polos se expresan como
Dependiendo del valor ξ, los sistemas de segundo orden presentan distintos comportamientos.
Excepto para ciertas aplicaciones en las que no se pueden tolerar oscilaciones, es conveniente que la respuesta transitoria sea suficientemente rápida y amortiguada. Por tanto, para una respuesta transitoria conveniente de un sistema de segundo orden, el factor de amortiguamiento relativo x debe estar entre 0.4 y 0.8; valores pequeños con una x <> 0.8 nos responderá con lentitud.
Dichos parámetros los podemos ver representados en la siguiente gráfica:
Tiempo de subida (tr): Tiempo necesario para que la respuesta pase del 10 al 90% de su valor final en sistemas sobre amortiguados, del 0 a 100% en sistemas sub amortiguados de segundo orden
Tiempo de pico (tp): Tiempo hasta que la respuesta alcanza el primer pico de sobre elongación
Sobre impulso Mp : Tiempo hasta que la respuesta alcanza el primer pico de sobre elongación
Tiempo de establecimiento (ts): Tiempo que se requiere para que la curva de respuesta alcance un rango alrededor del valor final del tamaño especificado por el porcentaje de la tolerancia admisible
Simulación del circuito RLC
Datos obtenidos del matlab
%Dando valores a los parametros.
C=0.00001;
R=63;
L=0.01;
%Desarrollamos los Polinomios.
num=[1/(L*C)];
den=[1 R/L 2/(L*C)];
g1=tf(num,den);
figure(1)
step(g1)
» RLC
Transfer function:
1e007
--------------------
s^2 + 6300 s + 3e007
»
Datos obtenidos teóricamente
Función de transferencia obtenida
Tiempo de subida (tr):
Tiempo de pico (tp):
sobreimpulso Mp:
Tiempo de establecimiento al 2% (ts):
Tiempo de establecimiento al 5% (ts):
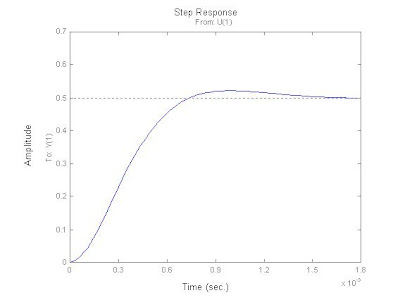
GRAFICO DE LA RESPUESTA TRANSITORIA DEL CIRCUITO
Datos obtenidos en el laboratorio:
MATERIALES UTILIZADOS EN EL LABORATORIO:
- POTENCIOMETRO DE 1KW
- INDUCTANCIA DE 10mH
- CONDENSADOR DE 1pF
TENSIÓN DE SOBRE IMPULSO (100%) = 45V
TIEMPO DE ESTADO ESTABLE = 12.8mseg
TIEMPO DE SOBREIMPULSO = 1.8mseg
TIEMPO DE ESTABLECIMIENTO (5%) = 6mseg
TIEMPO DE ESTABLECIMIENTO(2%) = 9.2mseg







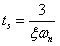






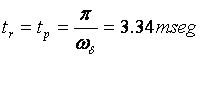





No hay comentarios:
Publicar un comentario